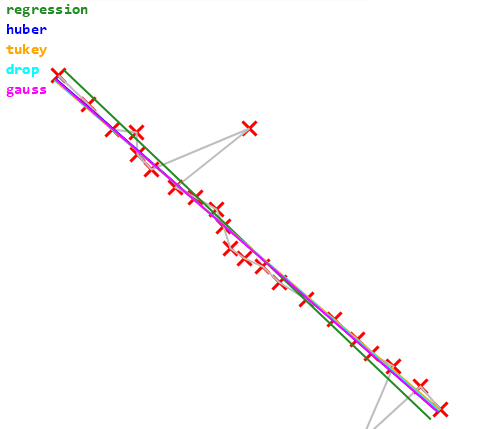
以拟合直线为例，分析总结几种方法，有最小二乘法、Ransac、Tukey、Huber。

image-20230701111935103

最小二乘法(Least Squares Method)

一种常用的参数估计方法，用于拟合数据点集到一个数学模型。它的目标是找到最优参数，使得模型预测值与实际观测值之间的残差平方和最小化。 在直线拟合问题中，最小二乘法可以用于找到最优的斜率和截距，使得直线与数据点的残差平方和最小化。 最小二乘法的优点是简单直观，但对异常值敏感。 demo1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include <iostream>
#include <vector>
#include <cmath>

// 直线结构体，包含斜率和截距
struct Line {
    double slope;
    double intercept;
};

// 最小二乘法直线拟合
Line leastSquaresRegression(const std::vector<double>& x, const std::vector<double>& y) {
    int n = x.size();
    double sumX = 0.0;
    double sumY = 0.0;
    double sumXY = 0.0;
    double sumX2 = 0.0;

    // 计算各项和
    for (int i = 0; i < n; i++) {
        sumX += x[i];
        sumY += y[i];
        sumXY += x[i] * y[i];
        sumX2 += x[i] * x[i];
    }

    // 计算斜率和截距
    double meanX = sumX / n;
    double meanY = sumY / n;

    double slope = (sumXY - n * meanX * meanY) / (sumX2 - n * meanX * meanX);
    double intercept = meanY - slope * meanX;

    // 创建直线
    Line line;
    line.slope = slope;
    line.intercept = intercept;

    return line;
}

int main() {
    std::vector<double> x = {1.0, 2.0, 3.0, 4.0, 5.0};
    std::vector<double> y = {2.0, 3.0, 3.5, 5.5, 6.0};

    Line bestFitLine = leastSquaresRegression(x, y);

    std::cout << "Slope: " << bestFitLine.slope << std::endl;
    std::cout << "Intercept: " << bestFitLine.intercept << std::endl;

    return 0;
}

demoCV

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include <iostream>
#include <opencv2/opencv.hpp>

// 直线结构体，包含斜率和截距
struct Line {
    double slope;
    double intercept;
};

// 最小二乘法直线拟合
Line leastSquaresRegression(const std::vector<cv::Point2f>& points) {
    cv::Vec4f lineParams;
    cv::fitLine(points, lineParams, cv::DIST_L2, 0, 0.01, 0.01);

    double slope = lineParams[1] / lineParams[0];
    double intercept = lineParams[3] - slope * lineParams[2];

    Line line;
    line.slope = slope;
    line.intercept = intercept;

    return line;
}

int main() {
    std::vector<cv::Point2f> points;
    points.push_back(cv::Point2f(1.0, 2.0));
    points.push_back(cv::Point2f(2.0, 3.0));
    points.push_back(cv::Point2f(3.0, 3.5));
    points.push_back(cv::Point2f(4.0, 5.5));
    points.push_back(cv::Point2f(5.0, 6.0));

    Line bestFitLine = leastSquaresRegression(points);

    std::cout << "Slope: " << bestFitLine.slope << std::endl;
    std::cout << "Intercept: " << bestFitLine.intercept << std::endl;

    return 0;
}

Ransac

RANSAC（RANdom SAmple Consensus）是一种用于估计模型参数的迭代方法，特别适用于数据集中存在异常值的情况。RANSAC的主要思想是通过随机采样形成的数据子集来估计模型参数，并通过计算内点的个数来评估模型的拟合程度。

RANSAC算法的基本步骤如下：

  1. 从数据集中随机选择一个最小子集（取决于模型的参数数量），该子集被认为是内点集合。
  2. 使用所选内点集合来估计模型的参数。
  3. 对于剩余的数据点，计算它们与估计的模型之间的距离或误差。这里的距离度量取决于具体的问题和模型。
  4. 根据设定的阈值，将与估计的模型具有足够小误差的数据点划分为内点，其他数据点划分为外点。
  5. 如果划分为内点的数据点数目大于某个预定义的阈值，即达到一定置信度，则将当前估计的模型参数视为最终结果；否则，返回第1步，重复迭代过程。
  6. 重复执行若干次迭代，选择具有最大内点数目的模型作为最终的估计结果。

RANSAC算法的关键之处在于它使用了随机采样的方式，通过迭代过程选择具有最大内点数目的模型。这种方法对于数据集中存在异常值或噪声的情况具有较好的鲁棒性，能够抵抗这些干扰因素，从而估计出较为准确的模型参数。

RANSAC算法在计算机视觉和机器学习领域广泛应用，例如图像配准、点云配准、线段拟合等问题。

demo1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
#include <iostream>
#include <vector>
#include <random>
#include <cmath>

// 直线结构体，包含斜率和截距
struct Line {
    double slope;
    double intercept;
};

// 计算直线与点的距离
double computeDistance(const cv::Point2f& point, const Line& line) {
    double distance = std::abs(line.slope * point.x - point.y + line.intercept) / std::sqrt(line.slope * line.slope + 1);
    return distance;
}

// RANSAC直线拟合
Line ransacLineFitting(const std::vector<cv::Point2f>& points, int iterations, double threshold) {
    std::random_device rd;
    std::mt19937 gen(rd());
    std::uniform_int_distribution<int> randomIndex(0, points.size() - 1);

    Line bestFitLine;
    int maxInliers = 0;

    for (int i = 0; i < iterations; i++) {
        // 随机选择两个点
        int index1 = randomIndex(gen);
        int index2 = randomIndex(gen);

        cv::Point2f point1 = points[index1];
        cv::Point2f point2 = points[index2];

        // 计算当前模型参数
        double slope = (point2.y - point1.y) / (point2.x - point1.x);
        double intercept = point1.y - slope * point1.x;

        Line currentLine;
        currentLine.slope = slope;
        currentLine.intercept = intercept;

        int numInliers = 0;

        // 计算内点个数
        for (const auto& point : points) {
            double distance = computeDistance(point, currentLine);
            if (distance < threshold) {
                numInliers++;
            }
        }

        // 更新最优模型参数
        if (numInliers > maxInliers) {
            maxInliers = numInliers;
            bestFitLine = currentLine;
        }
    }

    return bestFitLine;
}

int main() {
    std::vector<cv::Point2f> points;
    points.push_back(cv::Point2f(1.0, 2.0));
    points.push_back(cv::Point2f(2.0, 3.0));
    points.push_back(cv::Point2f(3.0, 3.5));
    points.push_back(cv::Point2f(4.0, 5.5));
    points.push_back(cv::Point2f(5.0, 6.0));

    int iterations = 100; // 迭代次数
    double threshold = 0.1; // 内点阈值

    Line bestFitLine = ransacLineFitting(points, iterations, threshold);

    std::cout << "Slope: " << bestFitLine.slope << std::endl;
    std::cout << "Intercept: " << bestFitLine.intercept << std::endl;

    return 0;
}

RANSAC算法的结果可能因为随机采样的不同而有所变化。增加迭代次数可以提高算法的鲁棒性，但也会增加计算时间。内点阈值决定了被视为内点的距离阈值。

Tukey

Tukey算法，也被称为Tukey's biweight或Tukey's bisquare算法，是一种鲁棒的统计估计方法，用于减小异常值对估计结果的影响。它是通过对数据的加权来降低异常值的影响，同时保持对正常值的较好拟合。

Tukey算法的主要思想是将异常值的权重设为0，将正常值的权重设为非零的常数。这样，在估计模型参数时，异常值将对结果产生较小的影响，而正常值将对结果产生较大的影响。

具体而言，Tukey算法使用了一个称为Tukey's biweight函数或Tukey's bisquare函数的加权函数。该函数的定义如下：

如果|x| ≤ c，权重w(x)为：

\[ w(x) = (1 - (x/c)^2)^2 \] 如果|x| > c，权重w(x)为0。

其中，c是一个常数，被称为鲁棒性参数或切断值，用于控制对异常值的容忍程度。

Tukey算法的基本步骤如下：

  1. 选择合适的切断值c和迭代次数。
  2. 初始化模型参数，例如斜率和截距。
  3. 对于每次迭代：
    • 计算每个数据点的残差（观测值与模型预测值之差）。
    • 根据残差的绝对值，计算每个数据点的权重，根据Tukey's biweight函数计算。
    • 使用加权最小二乘法（权重乘以残差平方）估计模型参数。
    • 如果模型参数的变化小于某个收敛阈值，则停止迭代。
  4. 返回最终估计的模型参数。

Tukey算法在统计学和机器学习中广泛应用，特别适用于处理存在异常值的数据集，能够提供鲁棒的估计结果，并减小异常值对模型的影响。

demo1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
#include <iostream>
#include <vector>
#include <cmath>
#include <algorithm>

// 直线结构体，包含斜率和截距
struct Line {
    double slope;
    double intercept;
};

// 计算直线与点的距离
double computeDistance(const cv::Point2f& point, const Line& line) {
    double distance = std::abs(line.slope * point.x - point.y + line.intercept) / std::sqrt(line.slope * line.slope + 1);
    return distance;
}

// Tukey加权函数
double tukeyWeight(double residual, double c) {
    if (std::abs(residual) <= c) {
        double x = (residual / c) * (residual / c);
        return (1 - x) * (1 - x);
    } else {
        return 0.0;
    }
}

// Tukey直线拟合
Line tukeyLineFitting(const std::vector<cv::Point2f>& points, int iterations, double threshold, double c) {
    Line bestFitLine;

    for (int i = 0; i < iterations; i++) {
        // 随机选择两个点
        int index1 = rand() % points.size();
        int index2 = rand() % points.size();

        cv::Point2f point1 = points[index1];
        cv::Point2f point2 = points[index2];

        // 计算当前模型参数
        double slope = (point2.y - point1.y) / (point2.x - point1.x);
        double intercept = point1.y - slope * point1.x;

        Line currentLine;
        currentLine.slope = slope;
        currentLine.intercept = intercept;

        std::vector<double> residuals;
        for (const auto& point : points) {
            double distance = computeDistance(point, currentLine);
            residuals.push_back(distance);
        }

        // 计算加权残差平均值
        double medianResidual = 0.0;
        std::sort(residuals.begin(), residuals.end());
        int numPoints = residuals.size();
        if (numPoints % 2 == 0) {
            medianResidual = (residuals[numPoints / 2 - 1] + residuals[numPoints / 2]) / 2.0;
        } else {
            medianResidual = residuals[numPoints / 2];
        }

        // 计算权重
        std::vector<double> weights;
        for (const auto& residual : residuals) {
            double weight = tukeyWeight(residual / (6.0 * medianResidual), c);
            weights.push_back(weight);
        }

        // 加权最小二乘法估计模型参数
        double sumX = 0.0;
        double sumY = 0.0;
        double sumXY = 0.0;
        double sumX2 = 0.0;
        double sumW = 0.0;

        for (int j = 0; j < numPoints; j++) {
            double x = points[j].x;
            double y = points[j].y;
            double weight = weights[j];

            sumX += x * weight;
            sumY += y * weight;
            sumXY += x * y * weight;
            sumX2 += x * x * weight;
            sumW += weight;
        }

        double denominator = sumW * sumX2 - sumX * sumX;
        if (denominator != 0.0) {
            double slope = (sumW * sumXY - sumX * sumY) / denominator;
            double intercept = (sumY - slope * sumX) / sumW;

            currentLine.slope = slope;
            currentLine.intercept = intercept;

            // 计算内点个数
            int numInliers = 0;
            for (const auto& point : points) {
                double distance = computeDistance(point, currentLine);
                if (distance < threshold) {
                    numInliers++;
                }
            }

            // 更新最优模型参数
            if (numInliers > bestNumInliers) {
                bestFitLine = currentLine;
                bestNumInliers = numInliers;
            }
        }
    }

    return bestFitLine;
}

int main() {
    std::vector<cv::Point2f> points;
    points.push_back(cv::Point2f(1.0, 2.0));
    points.push_back(cv::Point2f(2.0, 3.0));
    points.push_back(cv::Point2f(3.0, 3.5));
    points.push_back(cv::Point2f(4.0, 5.5));
    points.push_back(cv::Point2f(5.0, 6.0));

    int iterations = 100; // 迭代次数
    double threshold = 0.1; // 内点阈值
    double c = 3.0; // Tukey算法参数

    Line bestFitLine = tukeyLineFitting(points, iterations, threshold, c);

    std::cout << "Slope: " << bestFitLine.slope << std::endl;
    std::cout << "Intercept: " << bestFitLine.intercept << std::endl;

    return 0;
}

Huber

Huber算法是一种鲁棒回归（robust regression）方法，用于处理具有异常值的数据。它在线性回归中常被用作替代最小二乘法（Ordinary Least Squares, OLS）的方法。

在回归问题中，最小二乘法通过最小化残差的平方和来拟合数据，但当数据中存在异常值时，最小二乘法的表现可能会受到很大的影响。与最小二乘法相比，Huber算法对异常值有更强的鲁棒性，能够更好地处理异常值对回归结果的影响。

Huber算法通过引入一个称为Huber损失函数的修正项来实现鲁棒回归。Huber损失函数是一个分段函数，它在残差较小的区域使用平方损失（类似于最小二乘法），而在残差较大的区域使用线性损失。这种分段的损失函数可以在一定程度上平衡对异常值和正常值的拟合效果。

具体而言，Huber损失函数可以定义为： \[ Lδ(e)= \begin{cases}\frac{1}{2}e^2 \quad if ∣e∣≤δ \\ δ(∣e∣−\frac{1}{2}δ) \quad if ∣e∣>δ \end{cases} \]

其中，e 是残差（观测值与预测值之间的差异），δ 是一个称为Huber阈值的参数，用于控制在何处转换为线性损失。

Huber算法的求解过程通常采用迭代的方式。它通过最小化Huber损失函数来拟合回归系数，并使用迭代加权最小二乘法（Iteratively Reweighted Least Squares, IRLS）来实现。在每次迭代中，根据当前的回归系数，计算残差，然后根据Huber损失函数的梯度和权重来更新回归系数。迭代过程会一直进行，直到收敛或达到最大迭代次数。

总之，Huber算法是一种鲁棒回归方法，通过使用Huber损失函数来抵抗异常值的影响。它在处理存在异常值的数据时具有良好的鲁棒性，并且在许多实际应用中被广泛使用。

demo1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
#include <iostream>
#include <vector>
#include <cmath>
#include <limits>

// 直线结构体，包含斜率和截距
struct Line {
    double slope;
    double intercept;
};

// 计算点到直线的距离
double distanceToLine(double x, double y, const Line& line) {
    return std::abs(line.slope * x - y + line.intercept) / std::sqrt(line.slope * line.slope + 1);
}

// Huber损失函数
double huberLoss(double e, double delta) {
    if (std::abs(e) <= delta) {
        return 0.5 * e * e;
    } else {
        return delta * (std::abs(e) - 0.5 * delta);
    }
}

// Huber回归函数
Line huberRegression(const std::vector<double>& x, const std::vector<double>& y, double delta) {
    int n = x.size();
    double minError = std::numeric_limits<double>::max();
    Line bestLine;

    // 遍历所有点对
    for (int i = 0; i < n - 1; i++) {
        for (int j = i + 1; j < n; j++) {
            // 计算斜率和截距
            double slope = (y[j] - y[i]) / (x[j] - x[i]);
            double intercept = y[i] - slope * x[i];
            
            // 创建直线
            Line line;
            line.slope = slope;
            line.intercept = intercept;

            // 计算误差
            double totalError = 0.0;
            for (int k = 0; k < n; k++) {
                double dist = distanceToLine(x[k], y[k], line);
                double loss = huberLoss(dist, delta);
                totalError += loss;
            }

            // 检查是否是更好的直线
            if (totalError < minError) {
                minError = totalError;
                bestLine = line;
            }
        }
    }

    return bestLine;
}

int main() {
    std::vector<double> x = {1.0, 2.0, 3.0, 4.0, 5.0};
    std::vector<double> y = {2.0, 3.0, 3.5, 5.5, 6.0};
    double delta = 1.0;  // Huber阈值

    Line bestFitLine = huberRegression(x, y, delta);

    std::cout << "Slope: " << bestFitLine.slope << std::endl;
    std::cout << "Intercept: " << bestFitLine.intercept << std::endl;

    return 0;
}

demoCV

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include <iostream>
#include <opencv2/opencv.hpp>

// Huber回归函数
cv::Vec4f huberRegression(const std::vector<cv::Point2f>& points, double delta) {
    cv::Vec4f lineParams;
    cv::fitLine(points, lineParams, cv::DIST_HUBER, 0, delta, 0.01);

    return lineParams;
}

int main() {
    std::vector<cv::Point2f> points;
    points.push_back(cv::Point2f(1.0, 2.0));
    points.push_back(cv::Point2f(2.0, 3.0));
    points.push_back(cv::Point2f(3.0, 3.5));
    points.push_back(cv::Point2f(4.0, 5.5));
    points.push_back(cv::Point2f(5.0, 6.0));
    
    double delta = 1.0;  // Huber阈值

    cv::Vec4f lineParams = huberRegression(points, delta);

    double slope = lineParams[1] / lineParams[0];
    double intercept = lineParams[3] - slope * lineParams[2];

    std::cout << "Slope: " << slope << std::endl;
    std::cout << "Intercept: " << intercept << std::endl;

    return 0;
}